There is some debate online concerning hyperthreading and whether its good or bad. How many computational CPUs can I use on Amazon Webservices, etc. The thing is that all these reports are correct for their given benchmark case: the most important benchmark is the benchmark for you, which will vary in combination with both the hardware you are using and the software/model you wish to run.
Therefore, this is the first in a series of benchmark cases on some of the problems that I’m working on.
In this case the key details of my model are:
- OpenFOAM
- simpleFoam steady simulation for 2000 iterations
- kOmegaSSTLowRe turbulence model
- two-dimensional simulation with approximately 300k cells
- Reynolds number of ~200k
And the hardware that I’m testing on will be an AWS c4.8xlarge, which according to the specifications has 60GB of RAM and 36 vCPUs, namely, Xeon E5-2666 v3 (Haswell) processors. AWS notes that:
Each vCPU is a hyperthread of an Intel Xeon core…
As I interpret this then this is the hardware equivalent of 18 physical cores each running two threads.
As this is a relatively small cell count model and based on previous experience with CFD-ACE I expected the following:
- not to scale out linearly as more cores are added, and;
- performance to drop off as cores become hyperthreaded past 18
but I was not sure what the different simple and scotch decomposition schemes would do. In theory scotch is a better scheme as it seeks to reduce inter-processor face cells, which in turn reduces the computational overheads. Therefore, scotch decomposed simulations should run faster.
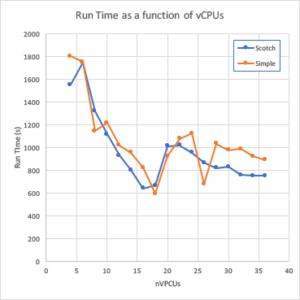
And that was the general trend of the observed runtimes, specifically:
- As more cores, up to 16, were added, run times decreased
- Run times decreased slower than linearly
- Run times increased beyond 18 cores
- Scotch simulations ran faster than simple decomposition
As shown below
The outliers however are very interesting. For the cases where simple simulations ran faster than scotch, 8, 16, 18, 22 and 24 vCPUs, the simple solutions reached convergence before the 2000 requested iterations. In contrast the remaining simple simulations ran for the full 2000 iterations. I have no real explanation for this save resorting to the fail-safe of dealing with non-linear numerical simulations on approximate grids.
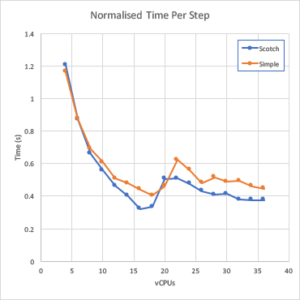
To account for the different convergent results, the run times can be normalised by the number of time steps to get and approximate of wall time per time step.
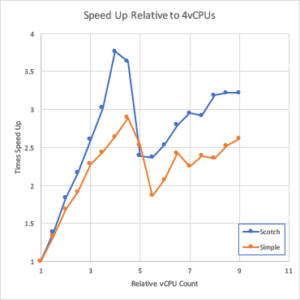
This is pretty much as would be expect and the scotch results are generally faster and that the performance drops off as more processor cores are added. An alternate visualisation strategy for this is to not look at time/step but at run time speed up.
In this case the reference point was the four vCPU case and for simulations up to 16 vCPUs, while the runtime does reduce, it reduces at a rate less than linearly. Now, this raises an interesting question: if throwing more CPUs at a single problem reduces in efficiency, is it better to run more jobs on fewer cores?
As it turns out the answer for this problem is that yes, it is better to run more jobs each using fewer cores. Using the data in the graphs above, we can compare the option of running four 18 core parallel simulations in series verses running four, four core parallel simulations in parallel.
| Large Job | Sub | |
| nJobs | 1 | 4 |
| nVCPUs | 18 | 4 |
| timePerStep | 0.3325 | 1.207326578 |
| nSteps | 2000 | 2000 |
| runTime/job | 665 | 2414.653157 |
| runTime Tot | 2660 | 2414.653157 |
And yes, in this case it is noticeably faster to run the four, four core jobs.
Finally, thanks for reading this article and please leave a comment below. If you are interested in being updated when similar items are posted then either subscribe via RSS or sign up to my mailing list below.